지난 시간 symmetry와 group theory 활용의 예로써 카이랄리티(광학활성)에 대해 얘기했고, 이번 시간에는 군론이 많이 쓰이는 분자진동할 것! 분자진동은 분광학적으로 얘기할 때 IR과 라만 분광학과 관련이 있다. IR, Raman은 분자 내 서로 결합을 이룬 원자들이 진동하게 되는데 이 진동 모드가 어떻게 되는지 군론을 통해 예상할 수 있다.

먼저 어떤 주어진 분자가 있을 때 진동모드의 계수를 간단히 알아낼 수 있다.
분자가 먼저 선형인지 아닌지에 따라 3N-6, 5로 바뀐다. (N= 분자 내 원자의 수 H2O 경우 H2개 O1개 총 3개 진동 모드를 갖는다.) 6와 5가 의미하는 게 뭐냐면.... 하나의 원자는 3방향으로 자유도 있고, N개 원자는 3N개의 자유도가 있다. 이게 곧 운동 방향(모드)가 된다. 3N개의 자유도가 있는건 3N개의 운동이 있다.(병진, 회전, 진동모드) 3N에서 전체 운동모드에서 병진과 회전운동을 제외하면 진동모드가 된다. 비선형 분자에서는 병진모드가 3개, 회전 모드가 3개 있고 선형에서는 병진 모드 3개, 회전 모드 2개가 있다. (병진모드는 전체분자가 한꺼번에 한 방향(x, y, z)으로 이동하는 것! 회전은 각 축(Rx, Ry, Rz)을 기준으로 해서 분자전체가 회전! 선형분자의 경우에는 병진운동은 동일하지만 회전은(Rx, Ry)로 Rz가 없다. 선형 분자 C∞v, D∞h경우 주회전축(z)으로 돌려도 C∞라서 변화가 없으므로 새로운 운동이 아니기 때문 Rz 를 제외한다.) 나중에 노말모드 분석에서 단계적으로 주어진 분자의 진동모드가 어떻게 얻어지는지 복잡한 과정으로 채워나가는데!! 단순히 진동 모드 수만 구하면 위 식으로 금방 알아낼 수 있다.
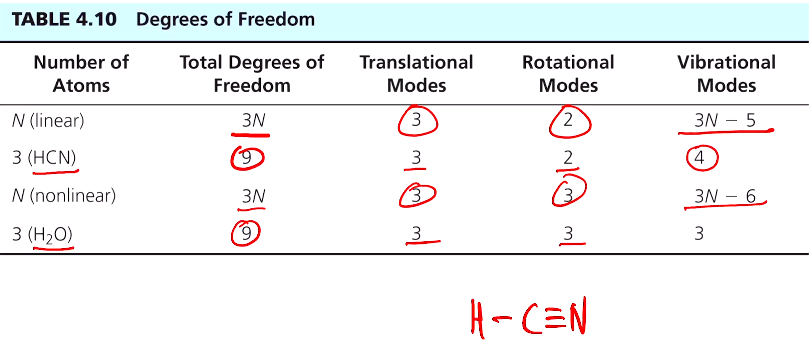
위 표를 보면 선형 분자의 경우 3N의 자유도가 있고, 곧 3N개의 운동모드가 있다는 것이다. 병진 3개 회전 2개다. HCN도 선형 분자로 N=3 으로 전체 9 개 중 3개는 병진, 2개는 회전, 4개는 진동모드다. 비선형 경우 전체 운동은 동일하게 3N개로 병진3개 회전3개이다. H2O 경우 비선형으로 전체 9개지만 병진, 회전, 진동 모드 모두 3개씩이다.
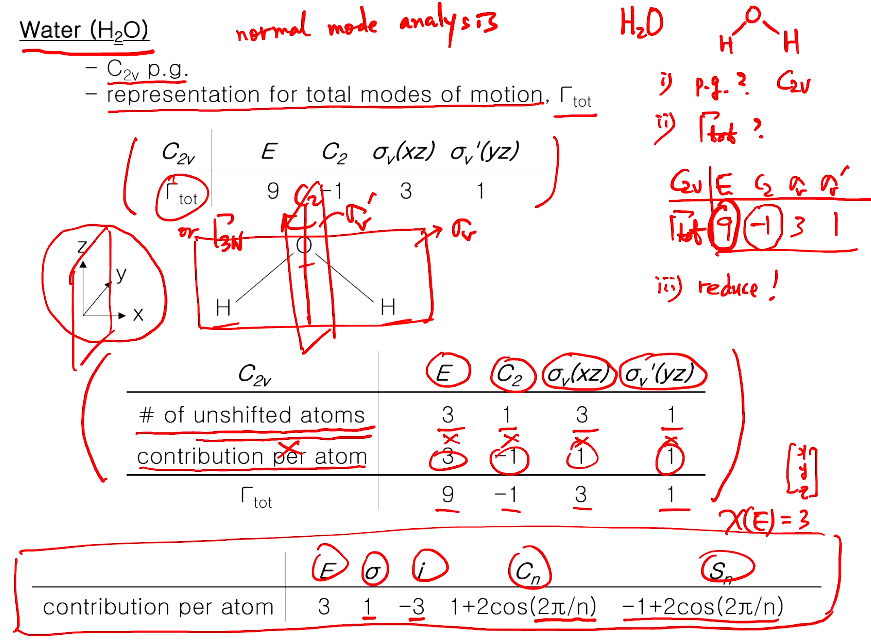
주어진 분자의 진동 모드를 어떻게 찾아나가는지 물 분자로 볼 것이다.
진동 운동 모드를 단계적으로 찾아 나가는 것을 normal mode analysis라고 한다. 진동모드가 많은 경우 독립적으로 하나만 일어나는 게 아니라 같은 symmetry의 진동모드가 서로 융합?믹스? 혼합?해서 일어난다. 그래서 기본이 되는 진동모드를 normal mode(정규 모드)의 진동모드가 어떤 건지 찾아가는 과정을 normal mode analysis라고 한다.
1. 가장 먼저 해야 할 것은 포인트 그룹을 찾기. 물 분자는 굽은 구조로 C2v!
2. Γ tot이 어떻게 되는지 찾아야 한다. Γ tot는 전체 운동모드에 대한 표현이다.
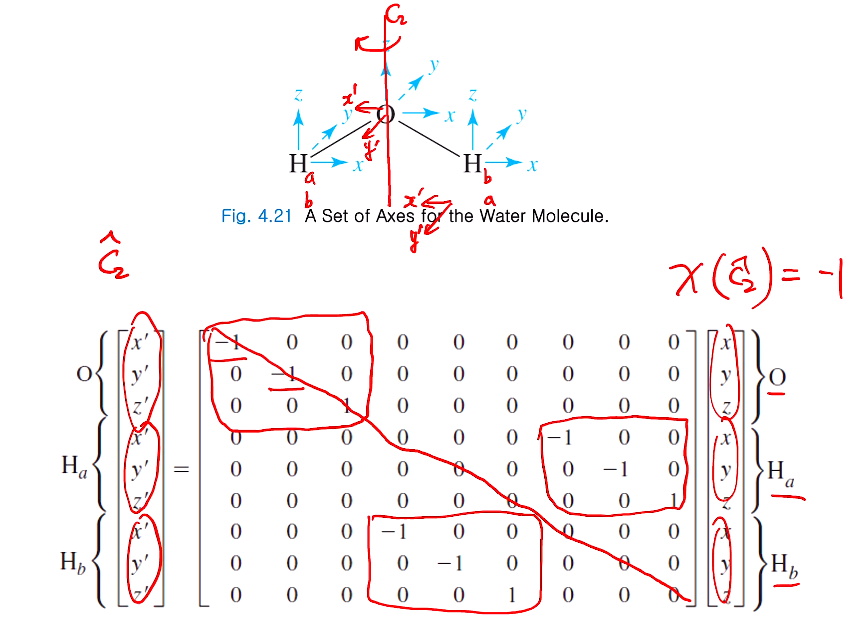
전체 운동모드는 C2v의 캐릭터 테이블을 보면 그룹 원소인 클래스별로 E, C2, sigma v, v'이 있는데, Γ tot (Γ3N)으로 표기하고 그 값을 캐릭터로써 어떻게 되는지 찾아나가는것! 어떻게 찾냐면! 다음 페이지에 물분자의 중심원자 O, z 축을 따르는 C2회전축이 있다.
- C2회전을 하면 z 축은 그대로 x', y'은 180도 이동하고 Ha, Hb의 자리 바뀐다. 바뀐 Ha, Hb의 x, y가 x',y'의 값을 갖게 되고 C2대칭 조작한 행렬을 나타내면 O, Ha, Hb의 원래 x,y,z가 있고 어떤 매트릭스를 곱해줘야 바뀐 O,Ha,Hb의 x', y', z'값을 갖게 된다. O는 자기 자리 그대로 있었으니까 x, y 값만 바꼈으니 x, y 쪽에 -1이 된다. Ha,b 는 서로 자리를 바꿨으니 더 이상 대각선 상에 있지 못하고 a가 b값이 됐으니 b는 a 값이 됐으니 위와 같이 대각선에서 벗아났다.
이 전체 매트릭스의 대각선 상의 0이 아닌 어떤 값을 갖지 못하게 된다. x(C2)sym op의 행렬의 캐릭터 값은 원자가 이동해서 대각선 상의 값이 없어서 기여를 못하고 이동하지 않은 O의 값만 -1, -1, 1이니 -1이 된다.

- 동등 E는 아무것도 안하니 따라서 모두 1으로 9가 된다. 원자가 3개 밖에 안되는데 이 그룹에 sym op에 대한 행렬을 구하면 9x9로 복잡하다...

그래서 이 방법으로 쉽게 구한다. 2- 1. 먼저 이동하지 않는 원자의 개수를 구한다. 위 E, C2, sigma v, v'가 그룹 내 원소로 sym op가 있고, 이걸 수행해서 이동하면 캐릭터 값이 더 이상 대각선에 남아 있지 않아서 기여 못 한다. 그래서 이동하지 않은 것만 고려한다. E는 아무것도 안 하니 구성 원자 3개가 모두 제자리! C2하면 H가 서로 자리 바꿔 O만 이동 안 한다. sgima v(xz)하면 세 개가 이동하지 않고 제자리에 있지만, sigma v'(yz)의 경우 O만 제자리에 있고 H는 서로 자리 바꾼다.
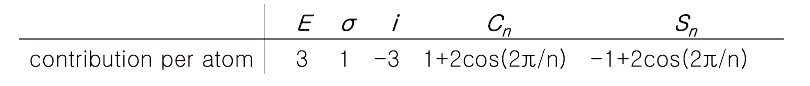
2- 2. 원자 당 기여도를 곱해주면 된다. 원자당 기여도는 정해져 있다. sym op 다섯 가지 는 정해져 있다. 이 값은 xyz를 basis 했을 때 캐릭터 값이다. χ(E)= 3 과 같이...값들이 정해져있다.

3. Γtot이 얻어지면 reduce하기 캐릭터 테이블에 있는 행에 해당하는 것은 이미 약분된 기약 표현이라고 했다. 방금 봤던 Γtot은 reducible rep이기 때문에 약분할 수 있는데 약분 식을 이용하여 약분한다. 기약표현의 합으로 약분한다.
Γr(R)=∑Γi(R)이다. 여기서 smal r은 red(가약) i는 irred(기약)!! 어떤 주어진 포인트 그룹에서는 기약표현은 정해져 있다. 물 경우 C2v포인트 그룹이고 기약표현은 4(A1,A2, B1, B2)개가 있다. 이런 기약표현이 몇 개로 이루어졌냐?... 기약표현의 합으로 나타낸다. 1번 기약표현이 몇 개가 있느냐!? 등 합으로 나타낸다. reduce한다는 것은 어떤 주어진 포인트 그룹의 특정한 irred rep의 수(ni)를 알아내는 것이다. 그 개수가 곧 특정한 irred의 개수가 red 속에 몇 개 있는지 알아내는 것으로 ni로 표기한다.?? ni= 1/h ∑Rχr(R)χi(R) (small r= red, i=irred, h: 차수) 어떤 특정 sym op에 있어서 해당하는 캐릭터 값이 red, irred 경우 어떤 값이냐~~거기에 sym op 같은 클래스 속에 nR을 곱해서 나타낸다. 모든 sym op C2v 에는 4개가 있고 다 더하면 된다./?..

물분자의 경우 Γtot red rep이 위와 같이 얻어졌다. 이걸 redce 한다는 것은 C2v 캐릭터 테이블 보면 4개(A1 , A2, B1, B2)의 irred rep이 red rep인 Γtot에 몇 개나 있는지 찾는다. A1 경우 h=4 nR= 모두 1이다. red rep의 모든 sym op은 E, C2, sigma v, v'이 있다. E의 nR=1, red rep=9, irred rep (character)=1 와 같이 C2, sigma v, v' 도 계산할 수 있다. nA1= 1/4[9 -1 + 3 + 1] = 3 만약 정수가 나오지 않는다면 잘 못 계산한 것! Γtot = 3A1+A2+3B1+2B2 처럼 나오면 reduce를 완료한 것이다.

4. Γ vib?? 진동 모드를 찾기 전체 운동모드에 대한 표현을 알아내고 즉, reduce해서 어떤 기약표현들의 합으로 이루어졌는지 알아내면 그 중 병진, 회전 운동 모드를 제외하면 진동 모드를 알 수 있다. Γvib= Γtot-Γtrans-Γrot Γtrans : basis가 x y z 에 해당하는 Γi이다. C2v 포인트 그룹에서는 x에 대한 것은 B1, B2이고, z에 해당하는 것은 A1이다 Γrot : basis가 Rx, Ry, Rz에 해당한 Γi이다. Rx=B1, Ry=B2 Rz=A2이다. Γtot = 3A1+A2+3B1+2B2 에서 병진(A1 B1, B2)과 회전 (B1 B2 A2)을 빼면 물분자의 진동모드는 2A1 + B1 러 3개(3N-6)임을 알 수 있다. 원레 전체 3N-6임을 알았지만 이게 어떤 symmtry, 기약표현, 밀리컨심볼의 진동모드인지는 몰랐는데 normal mode analysis 하니 알 수 있다.
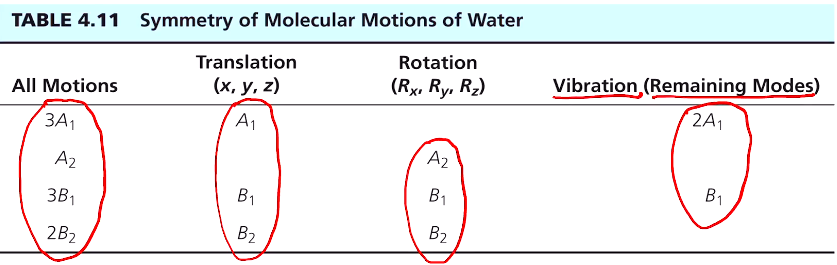
다시 정리해보면 위와 같은 표로 나타낼 수 있다. 물분자에서 전체 운동은 3A1+A2+3B1+2B2 로 9개가 있고 3개는 A1 B1, B2 병진, 3개 B1 B2 A2 회전을 빼면 3개만 진동모드인줄 알 수 있다.
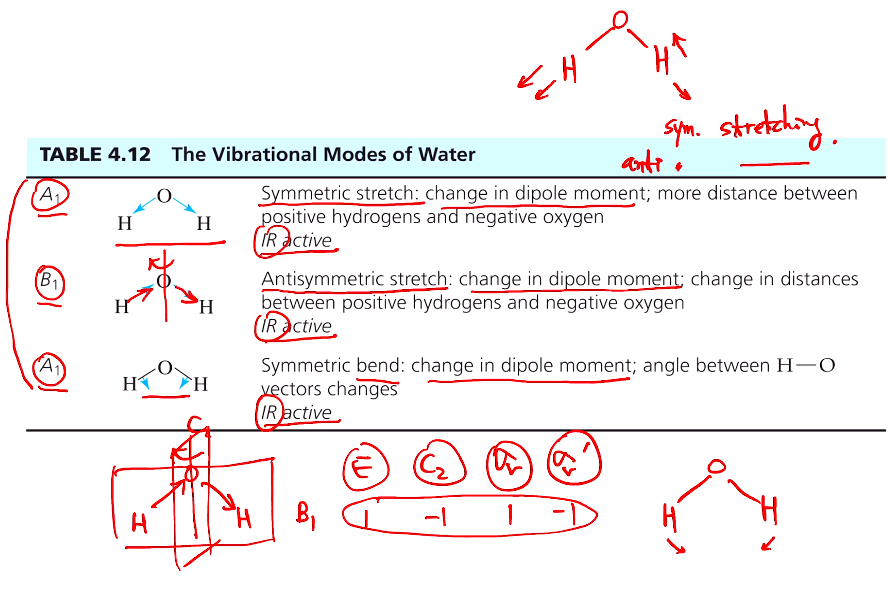
우리가 알고 있는 것처럼 물 분자를 그렸을 때, OH결합이 같이 늘어났다 줄어들었다 하는 symmetric stretching이 있다! 결합길이가 어느 하나는 늘어나고, 어느 하나는 줄어드는 antisymmetric streching 이 있다. A1은 symmetric stretching 한다! B1는 antisymmetric streching 하고 E를 하면 그대로인데 C2를 하면 서로 바뀌어 -1이 되고 sigma v는 자기 위치 그대로니까 1이고 sigma v'는 늘어나고 줄어드는 게 반대로 되어 -1이 캐릭터가 된다. A1는 bending도 한다. 결합각이 동시에 줄어들었다 늘어났다 하는 symmetirc한 운동한다. 이것 또한 symmetry을 따져보면 4개(E, C2, sigma v,v')의 sym op에 대해서 모든 캐릭터 값이 1인 symmetric 한 경우이다. 우리가 결과를 알고서 두 개의 OH결합이 어떻게 진동하는지 보였는데, 원자들이 어떻게 움직여서 진동하는까지 알기 위해서는 단순한 normal mode analysis로는 안되고, 내부 좌표(결합 길이, 결합각 등...)를 정의해서 따져야 하는데 여기서는 다루지 않을 것이다. 여기에서 보면 3개의 진동모드가 있는데 이들이 모두 dipole moment가 변하면서 IR Active 하다. 주어진 진동모드가 있을 때 IR! 활성인지?! 적외선 스펙트럼 얻을 때 스펙트럼에서 진동모드가 하나의 피크로 나타나는지 판단할 수 있다.