
symmetry and group theory로써
symmetry중 오퍼레이션이 포인트 그룹의 원소로써! 그룹이 갖고 있는 여러 가지 성질을 나타내는 거다. 원소들이 모여 그룹이 되기까지 4개 조건이 필요! 이 4가지 조건이 그룹의 성질!이다.
1. 동등 원소가 있어야 한다. 동등 조작 (E)
2. 원소의 역원소가 있어야 한다.
3. 그룹이 닫혀있어야 한다.
4. 결합법칙이 그룹 내 원소 사이에서 성립해야 한다.
교환법칙은 반듯이 성립해야 할 필요 없지만 결합법칙은 필수다.
실제 포인 그룹을 예를 들어서 왜 그룹이 될 수 있는지 확인할 것이다.
C3v 의 조건 4가지가 어떻게 만족시키는지 확인할 것이다.

1. 동등이 있냐 했을 때 동등 조작 (E)가 있고 이게 동등 원소가 된다. 모든 포인트 그룹에는 E가 있다.
C3v :
E, C3, C32 이 둘은 같은 클래스에 속해서 묶어 두 개의 C3가 있다 한다.
주 회전축을 포함하는 미러 플레인이 3개로 sigma v, sigma v', sigma v''이 같은 클래스에 속하므로 3 sigma v라고 한다. 총 6개 symmetry operation이 C3v group에 구성 원소가 된다. 6개 중 E가 있다는 게 첫 번째 조건 만족!
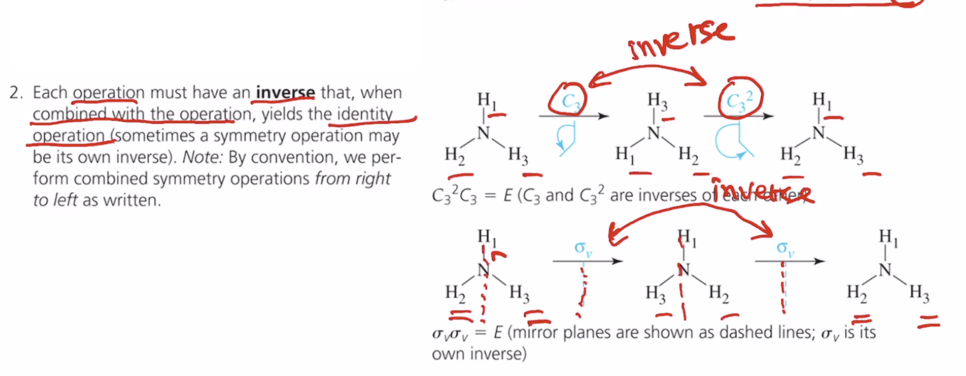
2. 각 오퍼레이션은 역이 있어야 한다. 역이라 하는 것은 자기에 곱해져서(곱해진다는 것은 연속적으로 수행한다는 것) 원래대로 돌아오는 또는 역을 곱했을 때 동등이 되는(원래대로 돌아오는)! C3가 있는데 여기에 C32를 하면 원래대로 돌아온다. C3 와 C32 는 서로 역이다. 각 원소의 역이 그룹 내 다 들어있다.
sigma v의 역은? 거울면이기 때문 또 sigma v 하면 원래 형태로 돌아올 것이다. sigma v의 역은 곧 자기 자신이다.
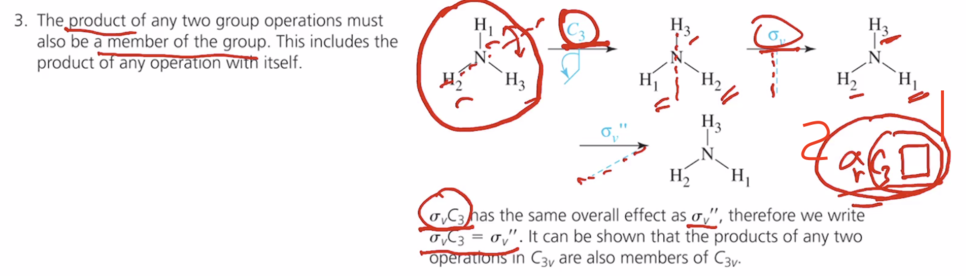
3. 닫혀있어야 한다. 그룹 내 원소인 어 떤 두 오퍼레이션을 연속적으로 수행하는 이런 프로덕트! 숫자에서의 곱하기랑은 다르지만 곱이라 한다! 곱한다는 것은 연속적으로 수행한다는 것이고 이랬을 때 또 다른 결과가 또 다른 그 그룹 내 멤버가 닫혀있다는 것이다. 어떤 둘을 연속적으로 수행했는데 얻어지는 결과가 그룹 내 원소가 아니면 닫혀있지 못하다고 한다. C3 , sigma v를 연속적으로 수행했을 때 sigma v '' 를 해야 원래 것이 얻어진다. sigma vC3 ☐라 했을 때 순서는 C3부터수행한다.

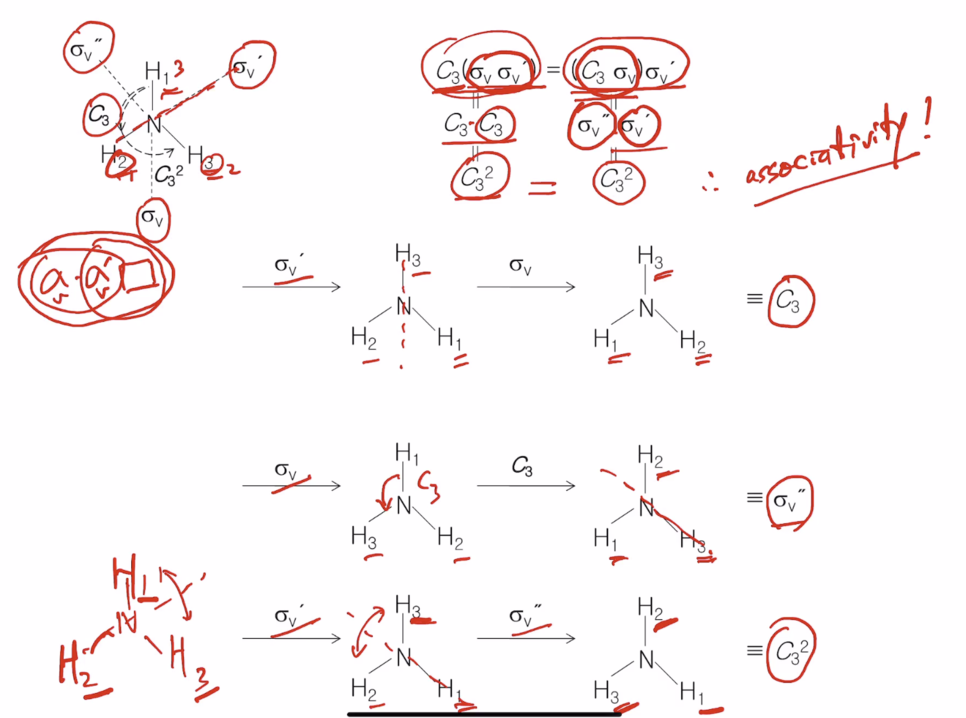
4. 결합법칙 associative property 가 hold 해야 한다. A(BC)=(AB)C
한 예로 C3v 그룹에서는 여섯 개 오퍼레이션 symmetry가 있는데 여섯 개 사이에서 모두 다 결합법칙이 성립해야 한다. 다 해볼 수 없으니 위 사진과 같이 세 개 해야 한다. C3(sigma v sigma v') =(C3sigma v) sigma v'
위 경우 왼쪽과 오른쪽 서로 같은지 보려면 각각이 어떤 결과를 도출하는지 찾아서 비교한다. 알아내기 위해서는 앞에서부터 임의로 서로 다른 수소 1,2,3로 구분하고 이들이 symmetry operation 했을 때 어떻게 숫자가 달라지는지 확인해보는 방법밖에 없다. 앞에 그림에서는 sigma v''이 반대쪽으로 되어있는데 반시계 방향으로 하면 위 그림이 맞다. 괄호를 먼저 해야 한다. 늘 오른쪽 먼저다. 계산을 하면 위 그림과 같이 계산하면 된다. 수소가 자기 자리에 있는 게 하나라도 있으면 sigma v 고 수소의 위치가 다 변했다면 C3일 것이다. 위 그림과 같이 결합법칙을 했을 때 왼쪽 오른쪽이 같음을 보이니 associative 성립하고 4번째 조건을 만족한다.
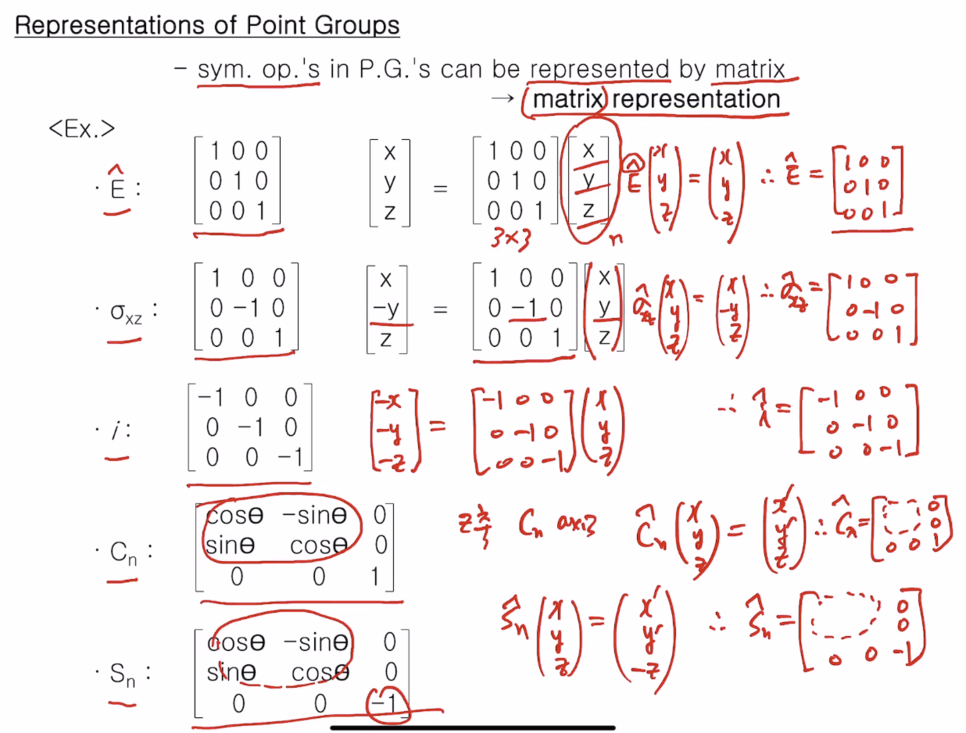
표현 레프리젠테이션은 symmetry opeartion을 매트릭스로 표현한다는 거에서 나온 용어이다. 즉, 어떤 포인 그룹의 구성 원소는 symmetry opeartiond들인데~ ! Sam op를 매트릭스로 나타낸 건데 이걸 매트릭스 representation이라고 한다. sym op는 동작, 움직이는 걸로 어떤 도형이나 어떤 값으로 나타내기 어렵다. 그것을 수치화하는 게 바로 매트릭스로 나타내는 것이다. 이걸 어떻게 나타낼 수 있냐~ sym op는 다섯 가지 op가 있었다. 동등 E, 반사 sigma, 반전 i, 회전 Cn, 반사회전 Sn 이들을 매트릭스로 나타내면 위 그림과 같다.
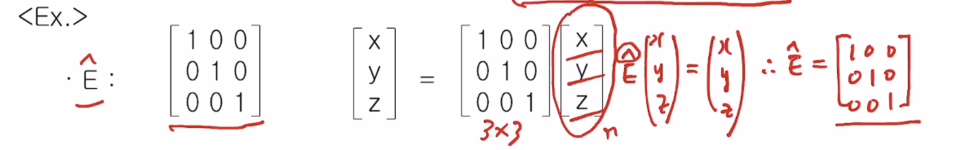
1. 동등은 아무것도 안한것! 그 좌표가 그대로 유지되는 것! x,y,z가 그대로 유지되어야 한다. (E 위의 삿갓은 이 symmetry가 sym op이다 sym elm가 아닌 것을 강조할 때) xyz변수가 3개인데 여기에 어떤 매트릭스를 곱해야 하냐면 3x3 행열 매트릭스로서 100, 010, 001을 곱해야 한다. E 는 xyz cordinate에서 위 그림과 같이 표현한다. 변수가 바뀌면 n x n 매트릭스가 될 것이다.
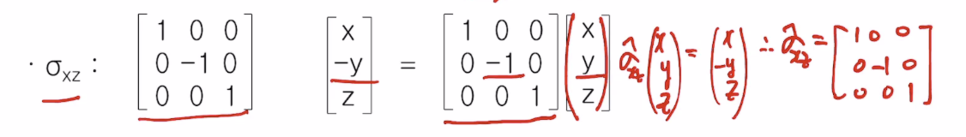
2. sigma xz cordiante에서 xyz 좌표에서 sigma xz 하면 xz 값은 그대로 있고 y 값만 바뀐다. xyz에다 어떤 매트릭스로 곱해져서 x-yz가 되려면 100, 0-10,001이 되어야 한다.

3. I 경우는 xyz 값이 모두 - 가 되어야 한다. -100,0-10,00-1가 되어야 한다.
물론 이 경우 xyz cordinate에서 변수가 3개일 때 해당된다.
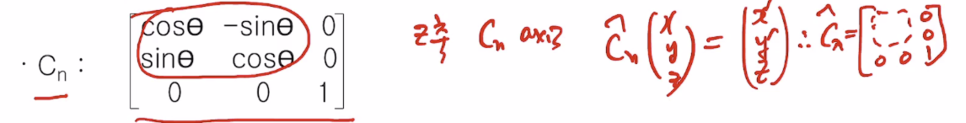
4. rotation axis는 조금 복잡하다. rotation axis의 축은 z 축이 Cn axis가 된다. 따라서 z 축값은 변하지 않는다. z값은 변하지 않으면서 x', y'이 되는 것이다. 뭔지는 모르지만 xx0,xx0,001이 된다. x는 삼각함수이다.
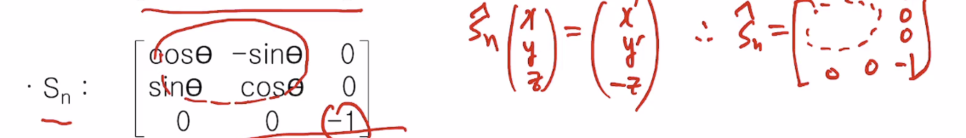
5.Sn의 경우는 Cn에 sigma h를 적용하기 때문에 Sn적용을 하면 x',y'가 되고 z는 - z값이 된다. sigma h 하고 Cn과 동일하니 삼각함수로 표시된다.
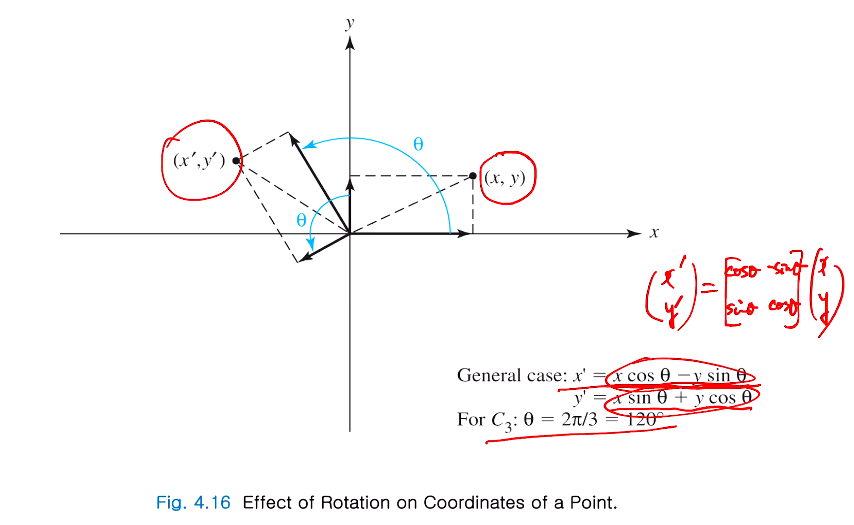
어떻게 Cn, Sn에서 xy에 해당하는 부분이 삼각함수가 되는지 알아보기 위해 위 그림을 보자! x,y 좌표가 x',y' 으로 로테이션 하는 각이 theta 만큼 회전했을 때
x'= x cos theta - y sin theta
y'= x sin theta + y cos theta
따라서 x', y'은 xy값에다가 위를 곱해준다!
주회전축이 C3라하면 θ가120도이다.
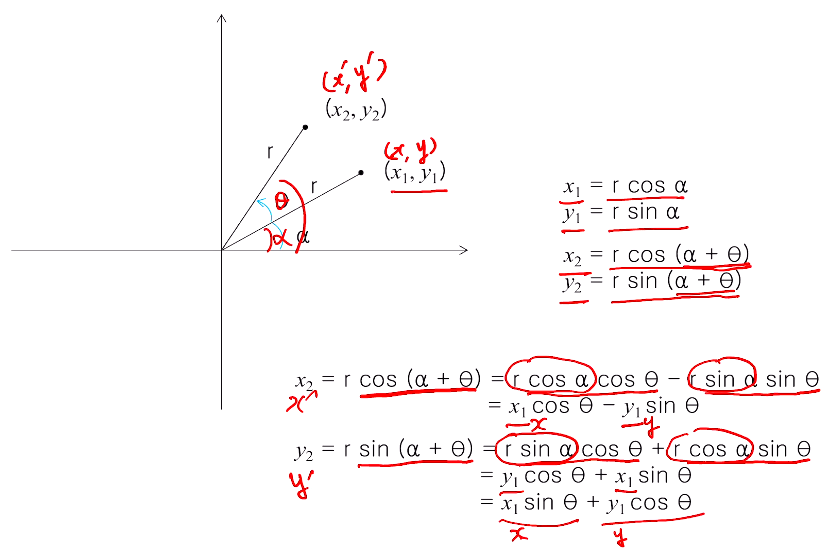
쉽게 코사인 관련 공식 쓰기 위해서 로테이션 각도가 90보다 적은 theta값을 갖는다 가정하고 원래 있던 좌표가 x1,y1 (x, y)이 있고 x2, y2 (x', y')으로 바뀌고 둘 사이의 어떤 관계인지 알아본다. 원래 좌표인 x1, y1은 거리 r cons alpha, r sin alpha 이렇게 된다. x2, y2 는 r cons alpha + theta, r sin alpha + theta 이다. 삼각함수 공식에 의해 정리하면 위 사진과 같이 된다.
(다시 볼 때 슬라이드에 x, y는 x1,x2, x', y' 등 같은 게 다르게 명명되어 복잡한데 그냥 딱 이해하듯 하면 될 듯 )

표현에 이어서 지표(Characters)에 대한 얘기를 할 것이다. 이 지표가 포인트 그룹 이론에서 어떻게 정의되는가 했을 때 matrix에 있어서 대각선 상의 성분들을 다 합친거가 지표이다. xyz좌표 축에서 매트릭스 representation 3x3였고, 이마저도 다루기 쉽지 않았는데 변수가 5~10개 면 상당이 큰 매트릭스라 다루기 힘들다. 대부분 다른 쪽에 있는 값들은 0이고 대각선 성분만 0이 아닌 숫자를 갖는데, 이 대각선 상에 있는 성분들의 합으로 어떤 매트릭스인지 유추할 수 있고 그래서 이걸 캐릭터라고 하자! Character (지표)의 기호는 χ(kai) 이다.
xyz 기준으로 했을 때 동등의 캐릭터는 3이다.
χ(σxz)=1, χ(i) = -3,
χ(Cn) = 2cos θ +1 (or 1 + 2 cos θ, 1+ 2 cos θ(2π/n))
χ(Sn) = 2cos θ -1(or -1 +2cos θ, -1+ 2 cos θ(2π/n) )
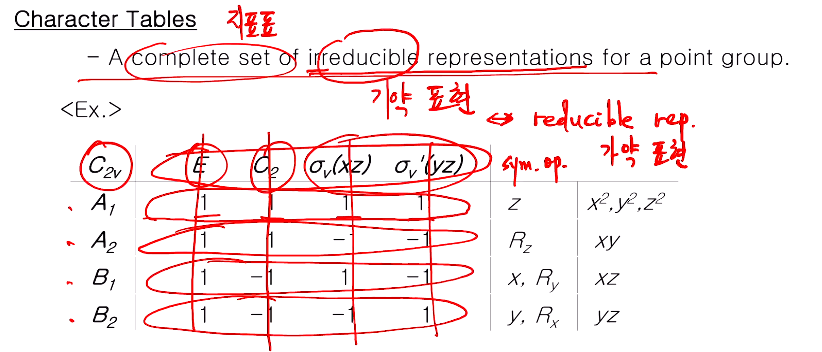
Character를 모아둔 테이블을 지표 표라고 한다.
숫자 하나하나가 캐릭터고 캐릭터들의 모임이 irreducible representations 라고 한다. 하나하나의 행이 기약 표현 ! reduce(약분)이 될 수 없는 것을 기약 표현이라고 한다. 반대는 reducible representation (가약 표현) 위 예시는 C2v 포인트 그룹의 캐릭터 테이블이다. 각 가운데가 지표고, 열에 해당하는 것이 C2v 포인 그룹의symmetry operation이다. C2v 의 구성 원소는 E, C2, sigma v, Sigma v'
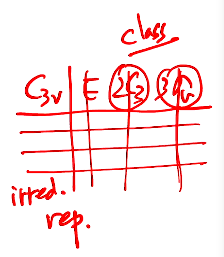

지표표를 보면 가운데 지표가 들어있고, 열에 제일 위는 sym op가 있고, C2v 의 경우 sym op가 하나씩 배정이 되어 있는데 다른 경우는 여러 개의 symmetry op가 묶여서 하나의 열을 대표하는 것을 볼 수 있다. 2, 3개 가 하나의 클래스에 속해 하나의 열에 놓인다. 행에 해당하는 irreducible representation이고 행에서 A1,A2,B1,B2 등 쓰는데 이건 밀리컨 심볼(mulliken symbol)이다.
기저 함수 basis function 이라 하고 일차함수와 이차함수 계통이 있다.

H2O로 예시를 들면 z축으로 C2, 모든 분자를 포함한 sigma v, 그의 수직한 sigma v' 는 위와 같다.
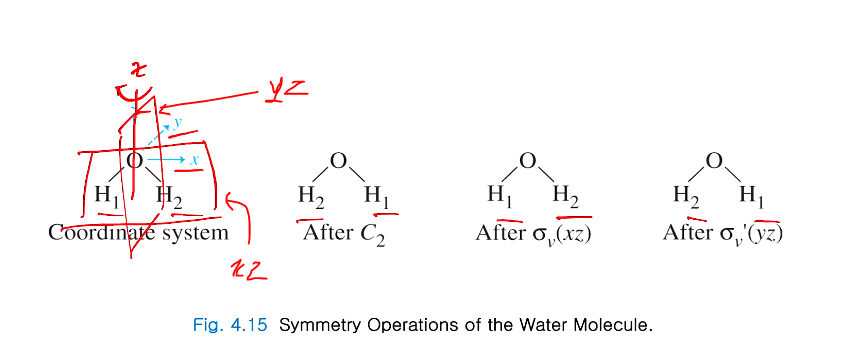
z축을 따라 C2 수행하면 H1,2 바뀌고 sigma v(xz)하면 앞뒤로만 바뀌지 옆이 안 바뀌고 sigma v'를 하면 좌우가 바뀌어 H1,2바뀐다.

뮬리컨 심볼(Mulliken symbols)
①. 1차 표현은 동등 조작 E 에 대한 kai 값이 1인 경우 A, B를 쓴다.
2차 표현은 동등 조작 E에 대한 캐릭터 값이 2라는 것으로 E를 쓴다.
3차 표현은 E에 대한 kai 값이 3으로 T를 사용한다. 나중에 eg t2g 오비탈 등 여기서 온 것이다.
②. 주회전축인 (Cn)=1 symmetric 한 경우 A라 한다. -1일 경우 B로 쓴다.
③. D그룹에서는 주회전축의 수직인 C2가 있는데 C2에 대해서 symmetrci이냐 antisymmetric이냐! 즉 kai 값이 1 or -1인지!
그다음 대칭성이 또 sigma v에 대해 1,-1인지 나뉜다. 1=> 1, -1=>2
3번까지로 밀리컨 심볼을 만들 수 있는데 복잡한 경우 더 나아간다.
④. inversion center에 대해 symmetric하면 g(gerade), 아니면 u(ungerade)이다.
⑤. sigma h에 대해도 symmetric 이냐 아니냐에따라 '. ''을 붙인다. 추가로 트리플도 있지만 기본적으로 이정도만!
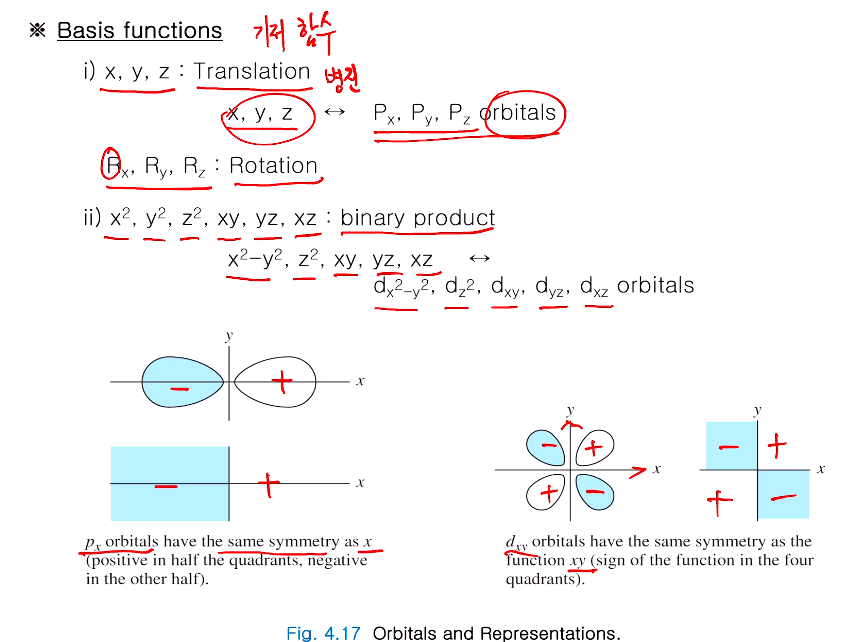
Basis functions (기저함수)
두 가지 영역이 있다.
첫 번째 영역에는 x,y,z, Rx, Ry,Rz가 있고 의미하는 것은! 나중 응용할 때 분자 진동 등! 운동모드를 얘기한다. x,y,z는 x,y,z 방향으로 병진운동이고 Px,Py ,Pz 오비탈에 대응되는 함수이다. x축 쌍으로 Px오비탈이 놓여있는데 그랬을 때 한쪽이 +면 다른 쪽이 - 다(그림). Px이나x 좌표는 같은 symmetry를 갖고 있고, xyz는 Px,Py ,Pz 오비탈에 대응된다. 그룹 이론이 대표적으로 적용되는 분야가 분자 이론 (molecual theory), 분자 진동이다. 분자 이론은 atomic obital(s,p,d...)들이 모여 몰레큘 오비탈이 어떤 basis function을 갖냐 할 때 Px,Py ,Pz 는xyz에 대응하고 운동모드 분자 진동을 얘기할 때 xyz가 병진운동을 한다. Rx, Ry,Rz 은 R이 x,y,z 축을 기준으로 회전(Rotation)하는 것이다.
두 번째 영역에는 2차함수 binar product 형태이며 x2, y2 , z2, xy, yz, xz 이것들은 d 오비탈을 나타내기 위한 것이다. x2 - y2 , z2, xy, yz, xz ↔ dx2 - y2 ,dz2, dxy, dyz, dxz orbital 이다. 그림과 같이 dxy, xy는 서로 같은 symmetry를 갖고 있어 대응되게 사용 가능하다. 기저함수들은 이걸 분자진동이나 궤도함수에 응용할 때 사용되는 내용이다.
'무기화학' 카테고리의 다른 글
| 무기화학 군론 [Symmetry and Group Theory (normal mode analysis, Γvib)] #15 (0) | 2021.12.15 |
|---|---|
| 무기화학 군론 [Symmetry and Group Theory(irred rep characters 7 properties, chirality) (0) | 2021.12.14 |
| 무기화학 군론 [Symmetry and Group Theory(point group)] #12 (0) | 2021.12.12 |
| 무기화학 군론 [Symmetry and Group Theory(point group)] #11 (0) | 2021.12.11 |
| 무기화학 군론 [Symmetry and Group Theory] #10 (0) | 2021.12.10 |