
최소 제곱법은 정량 분석에 있어서 통계를 적용시켜야 할 부분이 있다.
최소 제곱법은 교정곡선, 보정곡선 등을 그릴 때 여러 데이터 점들을 지나는 최적의 직선을 찾는 방법 중 하나다.
농도에 따른 흡광도를 점으로 농도에 따라 구하고 점을 찍고 그 점들을 이으면 직선이 있을 것이다. 그 점들은 이 직선에 가장 가까운 상태가 되게끔 직선을 구해야 하는데 이때 최소 제곱법을 쓴다. 실제 구할 때는 엑셀이나 데이터 가공해 주는 시그마, 오리진 등등 프로그램을 이용해서 구하면 아주 쉽게 값들을 구할 수 있다.
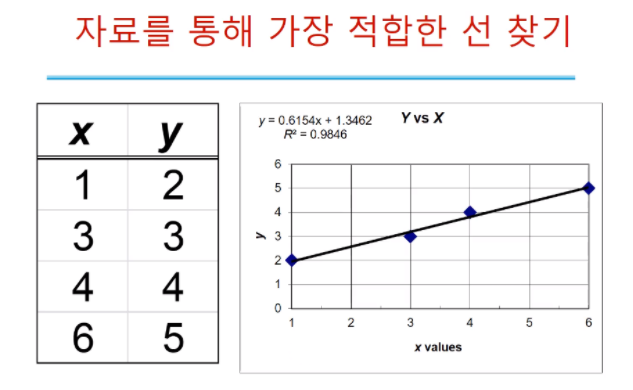
x(농도) 1일 때 y(흡광도)는 2이다 이런 식의 데이터가 얻어졌을 때 x,y 좌표상 위와 같은 점을 찍는다. 그리고 표준곡선으로 점에 가장 가까운 직선을 찾는 것이다. 직선이라고 하지만 교정 곡선이라고 한다. (이름의 교정이 붙은 점은 교정할 때 이 곡선을 쓰기 때문이다.) 임의로 긋는 게 아니라 계산 과정을 통해 선을 긋는다. R2은 점들과 직선이 얼마나 가까운가를 나타내며, 1에 가까울수록 실험에서 구한 점들과 계산에 의한 점들 대표하는 직선과의 연관성이 좋다.
항상 1보다 낮으며 완벽한 경우 1이 나온다.(보통 없음) R을 코릴레이션, 리그레이션(regression) 팩터로 부른다. 선형 회기법의 R을 따서 제곱한 값이 점과 직선과 얼마나 가까운지 보여준다. R2이 0.99 이상인 값만 쓴다면 실험을 잘 디자인해서 분석을 수행해야 한다.
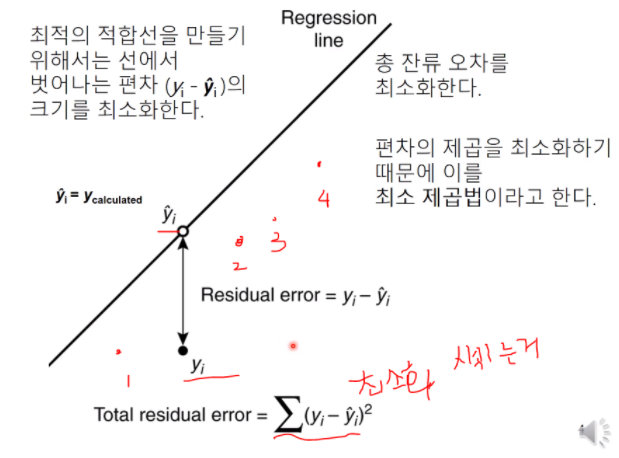
최소 제곱법 적용하는 원리를 보여주는 그림이다.
임의의 직선을 구하려고 한다면 데이터 yi가 있을 때 x값이 같은 직선상의 점y^i 차이가 error 가고 할 수 있다. 최소 제곱법의 해당하는 것은 그 차이를 제곱해서 최소화시키는 것이 최소제곱법이다. 근데 이런 포인트가 여러 개 1,2,3,4 등 있을 수 있고 그 차이를 다 합한 total residual error를 최소화시키는 직선을 찾는 과정이다.
'분석화학' 카테고리의 다른 글
| 분석화학 품질보증, 명세서 #15 (0) | 2021.10.06 |
|---|---|
| 분석화학 불확정도 계산 #14 (0) | 2021.10.05 |
| 분석화학 Grubbs 시험 #12 (0) | 2021.10.03 |
| 분석화학 가설 t 시험 #11 (0) | 2021.10.02 |
| 분석화학 student의 t, 신뢰구간 #10 (0) | 2021.10.01 |