
F테스트는 두 개의 표준편차를 얻었을 때 비교해서 차이가 얼마나 통계적으로 의미가 있는지! 통계적으로 표준편차가 서로 다르다, 다르지 않다를 판별하는 것!
건강검진을 할 때 한 곳의 병원에서 피를 뽑는데 열흘 동안 하루에 한 번씩 피를 뽑아 혈당 수치 측정한다. 혈당 수치에 평균과 표준편차를 보고 괜찮다고 느꼈는데 3 달 뒤 또 가서 10번을 열흘 동안 반복 측정해서 평균을 구한다. 병원에서는 3달 사이 방법은 같고 날짜만 다르며 3달 후 당뇨 수치를 비교해 볼 것! 10개의 평균들은 차이가 날 것 3달 뒤 당뇨 수치가 올라갔다! 이전 당뇨 수치와 비교했을 때 어떤 유의미한 변화를 보이는지 판단하고 싶어 하니까! 당뇨 수치가 올라가서 치료를 받아야 할지, 이 정도는 저번하고 비교해서 크게 문제없으니 정상적으로 생활할 때 어떻게 해야 할까? 같은 방법을 썼을 때 단순히 평균만 통계적으로 비교하면 됩니다.
만약 처음 A 병원에 3달 뒤 B 병원에 갔는데 두 병원에서 검사 방법이 다르면 각각에서 얻은 평균을 위와 같은 통계적인 방법으로 두 평균을 비교해도 되느냐? 결국 안된다.
A 병원에서만 얻은 평균과 A, B 각각 다른 방법으로 얻은 평균하고 다른 통계적인 처리를 해야 할 필요가 있다. 무조건 그런 건 아니지만 여기서는 서로 다른 통계적인 처리, 같은 통계적인 처리 중 뭘 해야 하나 결정하는 방법을 제시한다. S1은 A라는 병원에서 제시한 표준편차! S2는 B 병원에서 제시한 표준편차! 두 값의 비율을 가지고 F 값을 계산하고 테이블에 있는 F 값을 비교해서 테이블 보다 F 값이 크면!(S1이 더 큰 값으로 두는 거니까 F 값이 커지면 커질수록 두 표준편차 차이가 크다는 것!) 그렇게 될 때 어떤 기준값보다 F가 크면 이 표준편차는 차이가 크기 때문에 A, B 병원에서 얻은 평균을 비교할 때 A에서만 얻은 평균들을 비교할 때 다른 통계적인 방법을 써야 한다. 이런 결론을 내리는 과정에서 F 계산을 한다.
책에서는 경마장에서 경마의 혈중 탄산 수소이온 농도를 측정의 예를 들었다.
원래 사용하던 기기가 고장 나서 새로운 기기로 했을 때 측정과 표준편차는 위 표(4-2)에 있다. 이 두 개를 비교하고 싶을 때는 두 가지 방법이 있다. 표준편차 차이가 많이 나서 비율이 기준 값보다 큰 경우와 차이가 별로 안 나서 기준값보다 작은 경우는 비교하는 방법이 다를 수 있다. 평균값 비교는 뒤에서~ (표준 편차로 결정한다~) A와 B의 자유도, 9와 3이 만나는 F의 테이블 값보다 크면 동일한 모집단 표준 편차를 갖는 모집단으로부터 얻어졌을 가능성이 5% 미만이다...? F 값이 테이블 값보다 크고, 표준 편차의 차이가 너무 크다면.. 통계적으로 계산해보니 두 기기는 서로 모집단의 표준편차가 다르다는 이야기다. 즉, 다른 방법일 가능성이 있다. 그래서 평균값을 함부로 비교할 수 없다. 같은 표준편차를 주는 동일한 기기를 갖고 측정했을 때는 표준편차가 거의 같을 것이고 F=1이 될 것이다. 동일한 모집단 표준편차를 갖는 모집단으로부터 얻어진 것이다. 같은 방법이면 동일한 모집단 표준 편차를 갖는 모집단으로부터 데이터가 얻어진 가능성이 100%일 것이다. 다른 방법이면 위와 같은 방법으로 조사하여 F 값이 표 보다 크면 다른 모집단이라는 뜻! 다른 방법이면 표준 편차가 얼마나 다른지 보고(F 값 비교), 5% 미만이면 다른 방법의 평균을 비교할 때 방법이 달라야 한다. (표준 편차가 많이 차이 난다는 건, 비슷한 결과를 보일 것으로 간주하고 하는 건데? 3개월 뒤 달라질 수 있는 검사면 이 방법은 옳지 않아 보임. 같은 시각, 같은 컨디션에서 다른 방법을 썼을 때, 즉 결과가 같아야 하는데 표준편차가 차이 많이 나면 그 평균값을 비교할 때 다른 방법으로 해야 함.)
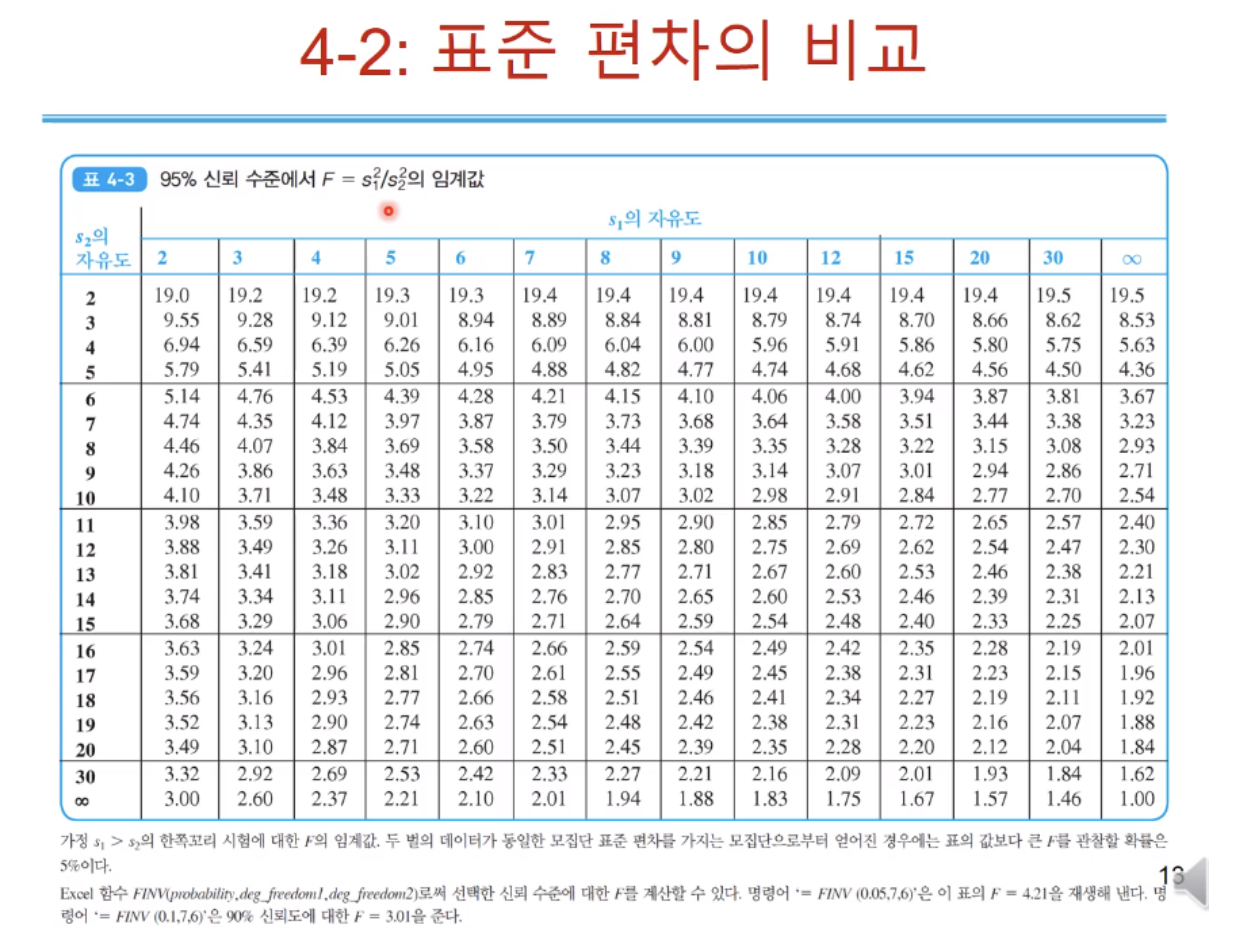
자유도는 n-1이므로 위 데이터로 보면 자유도가 9, 3이 될 것이며 둘이 만나는 3.86이 테이블 값이고 계산 값은 2.8로 테이블 값보다 F 값이 작으니까 서로 같은 모집단 표준편차를 갖는 모집단에서 데이터를 얻을 가능성이 높다.(5%보다) 평균값을 비교할 때 같은 방법으로 구한 평균을 비교하는 것과 같은 것을 쓰면 됩니다.

측정 횟수가 모두 13이라면 테이블 값보다 크므로 두 개 표준편차의 차이는 상당하다! 동일한 표준편차 모집단에서 얻은 데이터라고 생각할 수 있는 근거가 약하다
'분석화학' 카테고리의 다른 글
| 분석화학 가설 t 시험 #11 (0) | 2021.10.02 |
|---|---|
| 분석화학 student의 t, 신뢰구간 #10 (0) | 2021.10.01 |
| 분석화학 통계학 평균표준편차 #8 (0) | 2021.09.29 |
| 분석화학 통계학 가우스 분, 표준편차 #7 (0) | 2021.09.28 |
| 분석화학 계통오차의 불확정도 전파, 교정 #6 (0) | 2021.09.27 |