무기화학 군론 [Symmetry and Group Theory(point group)] #11

Symmetry and Group Theory 공부하는데 지난 시간은 Symmetry를 공부했습니다. Symmetry에는 대칭 요소(symmetry element) & 대칭 조작(symmetry operation)로 나눌 수 있고 operation은 그들이 구성 원소가 되어 그룹을 형성한다. 그 그룹이 일단 포인트 그룹이 되고 포인트 그룹 이외에 스페이스 그룹(공간군)에 구성원소가 될 수 있습니다. 포인트 그룹은! 어느 한 점은 고정되어 있는 그룹이다 해서 포인트 그룹이라 이름 붙여졌고, 그 점은 x, y 좌표상의 원점이다. 공간 군은 일반적으로 보는 대칭조작! 이 외에도 병진 조작이 추가로 있다. 그 대칭 조작들은 점이 고정되어 있지 않고 이동될 수 있다. 이른바.. 결정 구조에서 볼 수 있는 어떤 하나의 몰레큘이 연속적으로 배열이 되면서, 연속적으로 배열된 분자구조들 사이의 symmetry를 나타날 때 공간군이라하고, 독립된 분자를 놓고 대칭성을 따지고 그들이 어떤 그룹에 속하냐를 말할 때에는 점군을 얘기한다.점군에서 어떤 기준점이 x,y 좌표상 0점이고, 0점이 고정되어 있다는 뜻으로 포인트 그룹이라하고, 포인트 그룹은 크게 4가지로 나눌 수 있다. 물론 마지막 다섯 번째로 S그룹도 있는데 빈도가 낮아서 크게 4가지로 나눈다.

​

1. 저 대칭성 그룹

2. 고 대칭성 그룹

3. C 그룹

4. D 그룹

5. S 그룹 (빈도가 낮다.)

1. 저 대칭 그룹

symmetry operation이 하나 or 두 개 밖에 없는 그룹이다.

- C1: 동등한 E만 있는 대칭성이 없는 경우다.

- Cs: Sigma가 대칭 조작으로 미러플래인 하나만 있는 경우다. H2C=CClBr경우 평면으로써 전체가 같은 평면에 놓여있고 평면이 곧 거울 면이다.

- Ci: inversion center만 대칭 요소에서 비롯된 대칭 조작이다. 이 경우 ic만 있고 C-C사이 중간 지점이 inversion center이다.

2. 고 대칭 그룹

고대칭 그룹은 Td, Oh, IH, Th, O, I.. 등이 있는데 이들을 큐빅 포인트 그룹이라한다. 공동된 특징이 고차 회전축을 여러 개 갖고 있다.

- Td 경우 C3가 가장 고차 회전축이다. Oh는 C4가 3 개 있다. Td, Oh, Ih가 가장 중요하고 이들은 우리가 평소 봤던 기하구조이다.

기하구조 얘기할 때 소문자 td 쓰지만 포인트 그룹 얘기할 때 대문자 T와 소문자 d로 Td로 써야 한다. 기하구조가 사면체이다.

- Oh 경우 대표적인 예로는 SF6가 있다. 이 포인트 그룹은 Oh 포인트 그룹이다.

- Ih 경우 B12H122- 의 아이코사가 20을 얘기하고, 위의 5면 중간 10개 면, 아래 5개 면으로 20면체이다. 꼭지점은 12개다! 가장 고차원 회전축 C5 이 6개나 있다.

표에서 보겠지만 큐빅 포인트 그룹에는 Td, Oh, Ih 말고 다른 4개의 T, Th, O, I 그룹이 있다. 자연계에서 보기 힘들어 일반적을 보이는 Td, Oh, Ih가 대표적인 고차 포인트 그룹이다.라고 말한다. 표에는 추가로 C∞v, C ∞h 가 나왔는데 일반적으로 이들은 고차대칭성의 포인트 그룹으로 얘기하다 보다 C, D 그룹에 예로 말한다. 군 대칭성에 포인트 그룹에 포함할 수 있지만 일반적으로 C, D그룹의 일환으로 생각한다. C∞v, D ∞h 은 선형 분자다.inversion center가 없는 선형 분자는 C∞v 이고, inversion center가 있는 선형분자는 D ∞h이다.

Td 경우 C3 회전축이 4개 있고, 4개의 회전축으로부터 각 4개의 C3와 4개의 C32가 얻어져 총 8개의 C3 symmetry operation가 만들어진다. OT C4회전축이 3개가 있고 C4, C43로 총 6개 있다. Ih 경우도 6개 C5 회전축이 있고 C54 가 있는데 같이 묶여 12개의 C5가 된다. C52는 C53가 묶여서 12개가 된다. 각각 세로축? 칼럼들은 하나의 class가 된다. 같은 Class로 묶이면 대표 이름으로 합쳐져 표기된다. Td에서 sigma d? 미러?가 빠질경유 6S4, 6σd도 빠져버려서 8C3 가 C3, C32가 분리돼서 T 그룹이 된다.(같은 클래스 포함 x) T에 Sigma h가 3개 존재하게 되면 4S6, 4S65 이 추가로 만들어져 Th그룹이 된다.

O, I 그룹도 미러그룹 시그마가 빠지게 되면 분리되어 밑에 줄처럼 된다.

​

3. C 그룹

n겹 회전축으로서 Cn을 갖고 있는 그룹이다. n겹 회전축은 주회전축, 주축(main axis)라 한다. C 그룹은 3개의 그룹으로 나뉜다.

1. Cn: Cn만 있음

2. Cnv: Cn과 Cn을 포함하는 미러로 n 개의 "nσv" 를 갖는 놈! 이놈은 무한대 비갖는 선형 분자며 인벌전센터가 없는 C∞v가 있다.

H2O 분자는 Cnv그룹인데 위 그림과 같이 C2회전축을 포함하는 미러로 세워져 있는, 원자 3개를 포함하는 sigma v가 있다! 직교하게 존재하는 미러면은 sigma v'이라고 한다. 명명시 가장 많은 원자를 포함하는 경우 sigma v, 다음은 '(프라임)을 붙인다. NH3는 피라미달 구조로 회전축은 C3 로 N을 통과하며 H으로 이루어진 삼각형 중심을 지난다. C3 회전축과 N을 포함하는 면이 Sigma v이다. 또 다른 NH를 포함하는 면이 있고 동일한 원자 수를 포함하지만 어느 프라임은 임의로 정한다.

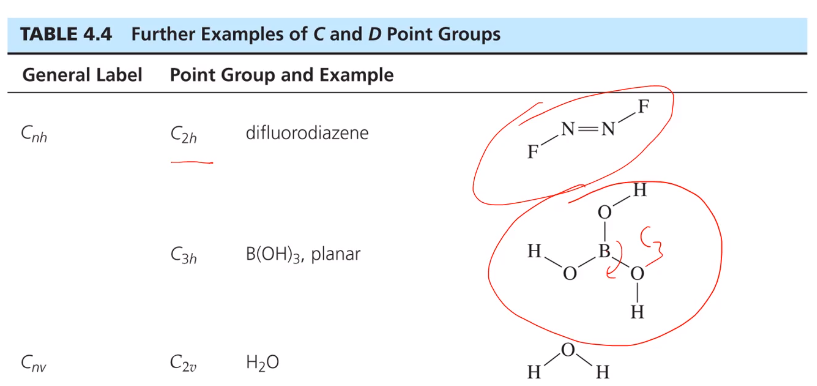
3. Cnh: Cn에 직교하는 σh를 갖는 Cnh가 있다.

Cnh의 예는 trans-N2F2가 있다. 트랜스로 평면 분자이고 N=N 결합 중심을 지나면서 회전하는 C2 회전축이다. C2 회전축에 직교하는 미러플래인으로 sigma h가 되고 C2h라고 표기한다. B(OH)3평면 분자이고 B를 지나는 회전축이 C3이고 여기에 직교하는 sigma h면이 존재하면 C3h 포인트 그룹에 속한다.

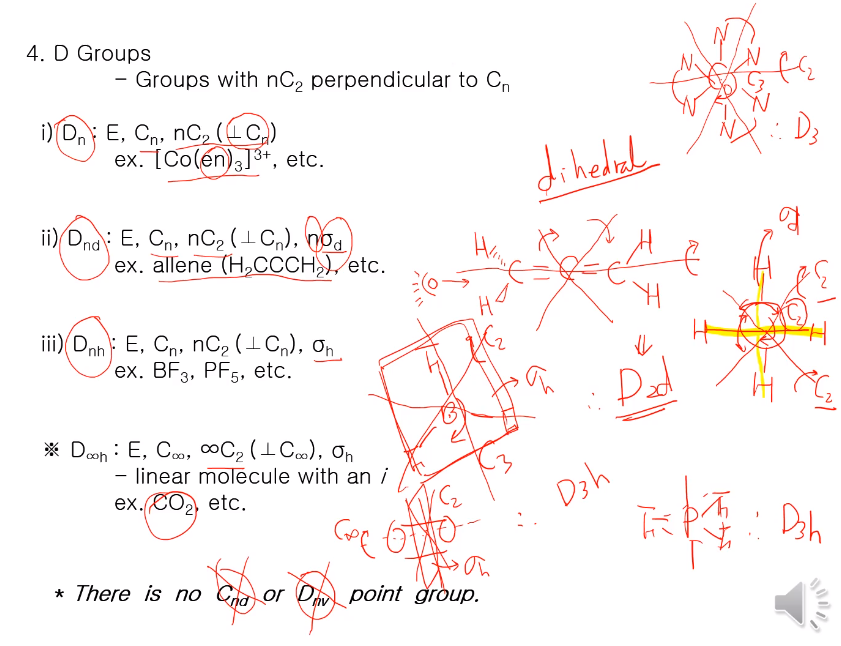
4. D 그룹

D 그룹은 주회전축 Cn의 직교하는 C2가 n개 있는 케이스다. D 그룹에도 3개의 부류가 있다.

​

1. Dn: Dn은 Cn과 Cn의 직교하는 n개의 C2만 있는거!

[Co(en)3]3+는 Oh구조로 중심 Co에 N이 고리처럼 연결되어 C3회전축이 있다. 중심 코발트를 통과하는 회전축에 고리 각을 이등분하고, 주회전축과 직교하는 C2가 3개 있다. D3에 해당된다.

​

2. Dnd: 1번 외에 sigma d 가 n 개 있는 것!

Dnd 알랜이 있다. 왼쪽 H는 앞뒤로, 오른쪽 H는 면에 놓여 있는 형태로 C2 회전축이 C를 따라 있고, 가운데 C를 통과하는 두 개의 회전축도 있다. 즉 직교하는 회전축이 두 개가 있어 D2회전축도 있다. 측면에 회전축은 수소의 (그림의 노랑 선) 미러플래인 각을 2등분한다. 미러플래인은 sigma v가 아니라 sigma d가 되는 것이다. 이 미러플래인은 주회전축 C2를 포함한다. C그룹에서는 sigma v였지만, 이와 동시에 C2로 이루어진 각을 이등분하는!!! 주 회전축 Cn의 직교하는 C2로 이루어지는 각을 이등분하는 미러플래인이 sigma dh이다.

알랜은 D2d 이다. 이런 미러가 없는 경우 Dn이다.

 

3. Dnh: 1번에 미러 h가 있으면 Dnh가된다.

BF3는 삼각형 기하구조로 B를 중심으로 C3회전축이 있고, 이 회전축에 직교하는 C2가 3개가 있다. D 그룹에 속하고, BF3면이 회전축에 직교하기 때문 D3h에 속한다. PF5도 삼각쌍뿔 기하구조로 D3h 그룹에 속함을 알 수 있다.

​

D∞n: 앞에서 선형분자의 경우 인벌전 센터가 있으면 D∞h이다. 이 경우 선형 분자로서 원통형 분자이기 때문에 원통형 가운데 중심을 지나서 회전축은 C∞ 고 양쪽 끝이 갖기 때문에 중간 가운데를 따라 무한대 개의 C2가 있다. 가운데를 자르면 sigma h가 돼서 D∞h 라한다. 하나하나 따지지 않아도 선형 분자로써 양쪽 끝이 같고 인벌전센터가 있으면 D∞h이다.

​

D 그룹에서 Cnd와 Dnv는 없고 Cn을 포함하는 미러는 sigma d 그룹이 된다.

sigma d가 Cn에 직교하는 n 개의 C2가 있을 때 C2로 이루어진 각을 이등분하는 그런 미러가 sigma d에 해당된다.

B(OH)3직교하는 C2가 없어 D 그룹이 못 되지만 미러플레인이 있어 h가 붙는다. PCl3도 삼각 피라미달에 3v가 되고 사각 BrF5피라미드는 C4가 있고 4개의 미러가 있으므로 C4v가 된다. C∞v로 HF, CO, HCN는 양쪽 끝이 다른 인벌전 센터가 없는 선형 분자들이다.주 회전축이 Cn이 있으면서 미러가 없는 건 C2이다. N2H4가 있는데 평면 분자는 아니고 N-N이 C2축이 되고 미러플레인, 인벌전센터 아무것도 없다. C3는 P(C6H5)3 는 트라이페닐포스핀 경우 페닐기가 포스핀 중심 원자에 결합되어 있는데 이경우, 위 그림과 같이 페닐기가 존재하여 어느 정도 지그러져 C3만 있고 미러들은 존재하지 않는다.

위에서 본 그림 말고 피라미달이 보이게 봤을 때 비공유 전자쌍이 있고 같은 평면에 놓인 기하구조는 아니고 미러가 있을 수는 없다.

D 그룹으로서 Dnh, Dnd를 볼 것이다.

PtCl42-의 경우 사각평면으로 C4가 있고, 직교하는 C2가 네 개 있다.

평면 분자로서 화면을 관통하는 게 주 회전축이고 직교하는게 평면으로 미러플레인 sigma h이다. 즉 C4h가 된다. Os(C5H2)2가 Cp 고리가 이클립스로 겹치면 어떤 메탈이든 모두 다 D5h가 된다.벤진은 6각형으로 가운데 기준으로 회전하여 C6이고 직교하여 C2가 6개 존재하며 C2를 포함하는 미러플렌이 자연스럽게 만들어지지만 또한, C6에 직교하는 미러플래인이 있냐? 하면 벤진 분자는 평면 분자로서 칠판을 관통하는 C6회전축에 직교하는 미러플래인 sigma h가 있다. 그래서 C6가 있고 6개의 C2가 C6에수직하고 sigma h가 있는 형태로 D6h이다. 이 직교하는 C2가 없어야 C그룹!!! D∞h 는 극한값? n이 무한대가 되는 것이다. D∞h는 양쪽 끝이 같은 이원자 분자 F2, N2 등 가운데 기준으로 갖고 인벌젼 센터가 있다 인벌전 센터가 있는 선형 분자는 D∞h가 된다.

Dnd그룹의 D4d 그룹은 Ni(cyclobutadiene)2(staggered) 정사각형 고리가 아래 위로 스태그드로 샌드위치되면 D4d다. 수직 방향으로 C4 회전축이 있고 수평쪽으로 C2 회전축 4개가 있고 미러플레인(C2에 각을 반으로 나누는 Sigma d)이 꼭짓점을 따라 4개 있다. 위에서 보면 슬라이드의 그림과 같다. 비슷하게 페로센 경우도 오각형(cp) 고리가 스태그드하게 샌드위치 되면 D5d 가 된다. 만약 이클립스로 있으면 D5h 가 된다. D3 에틸렌다이아민(NH2CH2CH2NH2. en)의 고리를 평면 고리라 생각하면 주 회전축 C3와 3개의 C2가 있고 미러가 없어 D3가 된다..

5. S 그룹

Sn 의 improper axis 또는 rotation reflextion axis 이 있는 것!!

다른 대칭 조작 요소는 없고 E, Cn , S2n이 있는 경우다. S2n의 예는 드물다. 위 예는 S4 그룹이다. 고리 중간을 지나는 C2 회전축이 있고 S4 회전축도 된다. 90도 돌려서 가운데 Sigma h로 반사를 시키면 같은 모양이 되기 때문!!! 포인트 그룹에 나타는 빈도는 매우 낮지만 이런 것도 있다!